A little disclaimer up at the top: I’m not a trained mathematician.¹ I will likely not use correct terminology, and I am certain that there are no new ideas here. Basically, don’t @ me.

I heard about the A Game By Its Cover Jam on the day it started. Wanting to look at some of the neat art that was created, I checked out famicase. I saw This Maze is Not Fair,² and it awakened something deep inside of me: the instinct to make an unfun maze game. Again.³

This time, however, I wanted to take it farther. I wanted to make an infinite perfect maze.⁴ One that was stable and consistent, so that following your path backwards would take you right back to where you came from, instead of generating the maze around you on the fly.

This, it turns out, isn’t an easy problem.⁵

Defining Maziness

Throughout this piece, I’m going to be using the terms “mazey” and “maziness” when I explain the decisions I make. This is the standard to which I’d hold a “good” maze for my purposes.⁶

So, what makes a maze “mazey”? Here’s how I would qualify the maziest maze:

• No correlation between the proximity of the cells and the distance (aside from a minimum distance as the crow flies).
• No repeating patterns that let you gather meta-information about the structure of the maze.

The closer a maze gets to meeting those two goals, the more mazey it is. A one dimensional line? Not at all mazey. A 2D maze generated by a proper maze generation algorithm? Quite mazey.

Generating Mazes

I’ve made a maze generator before.⁷ It’s easy. The algorithms are established, and they’re largely trivial to implement. They are, however, meant for filling up a confined space. You specify whatever grid structure you want⁸ and set it to work.

I tend to favor the recursive backtracker approach, which is quite simple.

1. Start at some cell.
2. Visit a random unvisited neighbor, adding it to the stack as you do so.
3. Repeat this process until you end up a cell without any neighbors.
4. Once that happens, get the top cell off the stack. If it has neighbors, continue from step 2. If it doesn’t, continue from step 4.
5. Once the stack is empty, you’ve fully explored the maze.

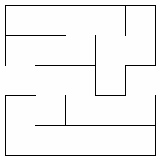
It’s easy and it makes an unbiased maze, which was desirable for what I wanted to accomplish. It also generates a perfect maze, which effectively means there’s only one path from one point to any other point (no loops).

The one thing it doesn’t do is support infinite mazes.

A Digression into Eller’s Algorithm

This is the point where more experienced mazers might point out Eller’s algorithm.⁹ It’s theoretically more performant than the recursive backtracker approach, as it does not need to keep the entire maze in memory, just the previous row and the generated row. It does this by keeping track of the sets that each cells is in. For a more in-depth approach, check the footnote on the start of the paragraph.

Perhaps the most interesting aspect of Eller’s algorithm is that it allows infinite mazes. Problem solved, right?

Unfortunately, no. There are two issues that prevent me from using Eller’s algorithm and calling it a day:

1. It doesn’t generate infinite mazes in more than one dimension. As long as one of the dimensions is fixed, it can generate infinitely in the other direction. Not a fit for an infinite 2D maze.
2. Generation has to begin at the top of the maze. You can’t start midway through¹⁰ and continue the generation from there, which is a problem if you want to generate both up and down infinitely using a naive approach.

Eller’s algorithm’s big advantage—only requiring a small amount of memory—ends up being moot for my use case, as I need to have the maze in memory to generate the mesh at runtime.

That’s not to say that Eller’s algorithm is less powerful than the recursive backtracker approach—it’s not—but for my purposes, which I chose doesn’t really matter.

Generating Big Mazes

The recursive backtracker approach is a sound one, but when we’re attempting to generate a very large maze (let alone an infinite one), we run into a very large problem: memory. At the very least, we need to keep track of the visited state for each cell. You could probably do some clever tricks to cut down on memory usage, but if we’re trying to generate this maze at runtime,¹¹ it’s going to take an increasing amount of resources.

What we need is something that allows us to generate chunks of maze at a time. If we could generate 25x25 chunks around the player on demand, it would dramatically decrease the amount of work we could do. For a very big maze, this is tricky: it’s possible that one pathway could go right for two million cells before doing a u-turn and coming back, but it’s hard to know that it would come back.

It turns out that there’s a straight-forward way to do this, but it does come at the cost of maziness.

Nesting Mazes¹²

Let’s put aside infinity for now.

Imagine we want to make a 10,000x10,000 maze. It would have 100m cells, which would eat up quite a bit of processing power and a fair share of memory.¹³ We would need to generate the entire maze at the same time, and we’d have no way of unloading parts of the maze from memory without it requiring a regeneration of the entire maze to restore it.

When mazes get large enough, it’s simply not feasible to keep them all in memory, nor is it feasible to generate the entirety of the maze once a chunk is unloaded.

Thankfully, there’s an easy solution: nesting mazes.

Think of a 3x3 maze.

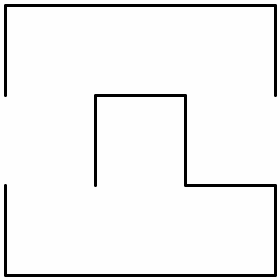
No matter what 3x3 maze you pictured, it’s trivial. There’s no complexity to it. We can, however, increase the complexity of our simple 3x3 maze by embedding 3x3 submazes¹⁴ in each cell of the maze. Suddenly, we have a 9x9 maze.

The nested 3x3 submazes inherit which sides they have exits on from the structure of their parent maze. The only communication that needs to happen between the submazes is to handle which on cell boundary the exit gets added.¹⁵

As many mazes can be nested as you want. For instance, 50x50 mazes could be nested inside 25x25 mazes which could be nested inside a parent 100x100 maze, making a whopping 125,000x125,000 cell maze.

Let’s think back to our original 10,000x10,000 cell maze. That same maze could be made up of 4 10x10 layers. Since each submaze does not require its neighbors to be generated, just its parents, we would only need to keep a 10x10 maze for each maze in memory, resulting in only 400 cells in memory.

There is, however, a downside. If you’re mapping the maze, you’ll notice that every 10x10 section of the maze will have between zero and one exits on each side, and that once you’ve traversed a submaze, you’ll never need to go back through any part of that submaze unless that submaze wasn’t part of the path to the exit.

Compare the above nested 9x9 maze to the non-nested one generated below.

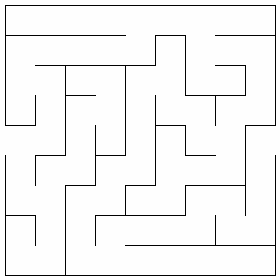
If you can hold the entire maze in memory, do so. You’ll end up with a mazier result. No matter how beefy of a computer you have, however, you won’t be able to hold an infinite maze in memory.

Infinitely Nesting Mazes

I said above that a submaze needs to hold all of its mazes in memory for generation. That isn’t entirely true. It only needs to generate its parents until it finds one that isn’t on the edge of its own parent maze, since the parent is only required to determine which sides of the submaze have an exit.

Let’s look back at our nested 3x3 maze for an example:

The parent 3x3 maze had to get its exits (left and right hand side) somewhere. Theoretically this parent maze could be the child of an even bigger nested maze. However, the cell in the center of our outer 3x3 maze doesn’t need to know its parent’s exits: it doesn’t touch any sides where an exit could be.

My first idea for generating an infinite maze was to nest infinitely, with each layer being nested even deeper than the last. From my explanation above, it’s probably simple to see where the flaw is: eventually you’ll cross a threshold that’s on the border of infinitely many mazes, which would take an infinite amount of time to compute and an infinite amount of memory to store.

To illustrate, assume we start with a 10x10 maze with its origin at (0, 0). We need to know if we’re on the edge of the parent maze, so we generate a 10x10 maze that contains us. However, since we’re at (0, 0), we’re also on the edge of the parent maze, so we generate its parent 10x10 maze. However, since we’re at (0, 0), we’re also on the edge of that parent maze, so we have to generate its parent. And so on and so forth. Since we’re always on the edge, we’ll have to generate parent mazes. Forever.

You can try to do things by moving around the origin, but as far as I know, you’re just moving the problem to some other point in space. Since we want to generate an infinite maze, we’ll run into that case eventually, and our program will be stuck generating parent mazes until it runs out of memory and crashes.

At this point, I got to wondering whether an actual infinite perfect maze was even possible.¹⁶

So, I tried to figure out a simpler case.

Generating Infinite Mazes… in 1D.

This is really easy. What’s an infinite maze in one-dimensional space? A straight line.

Is it the world’s most boring maze? Yes.¹⁷ Does it give me an idea? Yes. Do you see where I’m going? Probably.¹⁸

We can nest these to make an infinite 2D maze with one dimension of a fixed size.¹⁹

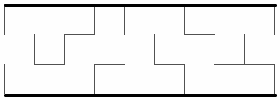
This still doesn’t allow us to use infinite nesting to reach infinity, but it does allow us to create an infinite 2D maze… at a cost.

But Pretending It’s 2D

At its core, the advantage that the 1D space gives us is letting us reach a point in the nesting process where we can say, without going up any further, where the exits are. Once we’ve reached that point, we’re set. We’ve reached a finite solution to the infinite problem.

Can we do the same for 2D? Yes, and it’s trivial. Nest as many mazes until you get to a satisfying supercell²⁰ and then connect it to every adjacent supercell. The cost is limited to one of each of size in the maze stack. The only problem with this is that you won’t generate a perfect maze.²¹

And I wanted perfection.

That left me with a new problem: how could I have some sort of procedural infinite pattern in which I knew every cell was reachable from any other cell by exactly one pathway? I needed a bridge from my nested maze to infinity.

My mind immediately went to something I’d done previously: space-filling curves.

Space-Filling Curves

Space-filling curves are curves (in this case, a collection of straight line segments) that will completely fill a 2-dimensional unit square.²² They wind in and out, eventually filling up the entirety of the space. These curves tend to be built as iterative functions. There are many of these such curves, one of which is the Hilbert curve. Here are the first few iterations:²³

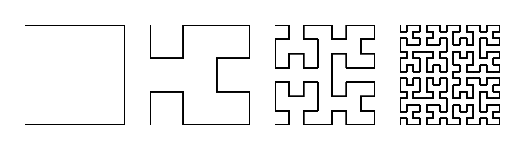
This approach seems ideal: these curves, while self-similar, have somewhat of a maze feeling. They mirror and rotate, forming complex patterns that leave you unsure of where you’d go next.

There are two potential problems with this approach that scared me away:

1. It’s a different “kind” of infinity. I’m looking for something in infinite 2D integer space, and this is inside the 2D unit square. I’m not sure those two 2D infinite spaces can be transformed between.
2. I’m not aware of any way to compute a space-filling curve’s adjacencies for a given point aside from an iterative function, which reminds me too much of my infinitely nested maze debacle above.

There may be ways to solve this problem,²⁴ but some cursory searching didn’t yield anything, and I didn’t want to spend a good deal of time looking into it only to find out what I already suspected—that it wouldn’t work.

Settling for a Spiral

While I was looking into space-filling curves, I had something in my back pocket: you can really easily turn a 1D line of cells into a 2D spiral of cells. The only problem with this is that it’s not an exciting pattern.

For one thing, for an increasing percentage of cases as you deviate from the center, you’ll just end up going in one direction to get to any destination far enough away. For another, the spiral has a start, which means that there’s a good chance that you can’t go in the wrong way forever.²⁵

I was able to address my second concern by using a bidirectional spiral.²⁶

As you can imagine, the texture of this one is quite apparent as well, but I satisfied my concerns by making each cell of the spiral contain more than 15,000 cells to a side. It still does have an apparent texture, but that’s due to the relatively small size of the base nested maze.

Is This Cheating?

It does feel I’m cheating my way to infinity. At its base level, there’s a pattern you can discern. I don’t know if there’s a finite-time alternative to the mechanism of using an “infinity bridge”²⁷, but ultimately, I doubt players can tell as they can’t see much of the maze at any time.

A large section of the maze would need to be mapped to suggest the spiral structure, and theoretically a spiral structure could appear in any truly random infinite top-level pattern, so you’d never really be certain.

I still wonder if some sort of fractal approach could apply, but I simply didn’t have enough time to do much research within the jam constraints I had. Hopefully someone will come along and come up with a great and mazier approach for infinite maze generation. I’d love to see it.

Could You Do This in 3D?

Yes, quite easily. I’m sure a spiral is extensible to 3D, and most maze algorithms work just as well in 3D, including my workhorse, the recursive backtracker. I suspect that you could make a spiral in even more than two directions in 3D, but I don’t have a whiteboard to try to draw it out. Something for someone even more sadistic than me, I suppose.

The End Product

I ended up finishing my game, THIS MAZE HATES YOU., with time to spare. I suspect that it was infinitely more fun to make than it is to play, but it does have a nice reward for reaching the end. The smallest submaze size is 25x25, which is quite apparent when looking from above, but harder to tell when in the maze. That was to minimize the maze generation time (although 50x50 probably would’ve been acceptable), and allow for easier chunking of maze mesh generation.²⁸

---

1. It might even be a stretch to call me an untrained one. ↩︎

2. This Maze is Not Fair was actually the second cartridge that inspired me, but we’ll see if I get around to making a game based on the first one. ↩︎

3. See The Instatiable Tomb of Ratakanen, a game I finished in mid May of 2022. ↩︎

4. A maze being perfect means that every pair of points has exactly one pathway between them. If this restriction was lifted, it’d be trivial to create infinite mazes: just connect every cell to every other one. ↩︎

5. Ultimately, though, it’s not exactly hard. ↩︎

6. Fun is explicitly not a metric I’m targeting. ↩︎

7. Proof. ↩︎

8. Rectangular, polar, hex, etc. ↩︎

9. For a better explanation and a better-written maze website, see here. ↩︎

10. You could theoretically create maze row “snapshots” to allow generating from that point, but that would end up taking more work than the approach I ended up landing with. ↩︎

11. Which we’d need to, since caching an infinite maze would require an infinite amount of space. Probably. Maybe there’s some clever math thing, but I doubt it. If there was, it could probably be used for infinitely good compression, which I’m sure I would have heard about. ↩︎

12. There’s probably a real name for this, but I couldn’t find it. ↩︎

13. Yes, Eller’s algorithm would do better here, but that’s not the point, I promise. ↩︎

14. There’s no requirement that a nested submaze and its parent have to have the same size: 3x3 was chosen purely to keep the full image size down while giving slightly more complexity than a 2x2 maze. ↩︎

15. Even this isn’t strictly necessary. In my game, each submaze determines the exit positions, if they exist, for the right and upper sides, and just rely on the mazes below them and on the left to build up the walls in those directions. ↩︎

16. Despite the ordering of this post, I wasn’t aware of Eller’s algorithm yet. Still, I wanted infinite bidirectional generation, not in a single direction, so I wouldn’t be satisfied. ↩︎

17. Actually, arguably, all infinite mazes are equally boring since they all take an infinite amount of time to get from one end to the other. Now if it was a finite 1-D maze, then it’d be the most boring maze. Well, actually, maybe not. A maze that took two seconds to complete would be considerably more fun than most other mazes, which tend to be anti-fun. Whatever. It’s a maze. ↩︎

18. Are these rhetorical questions overstaying their welcome? Definitely. Have I done this bit in a previous blog post? I think so. ↩︎

19. Once again, I was not aware of Eller’s algorithm when I was figuring this out, and having access to Eller’s algorithm would have probably led me down some time-consuming wild goose chases. ↩︎

20. What I call the biggest unit of a maze. e.g. for a 10x10 maze holding a 5x5 maze holding a 3x3 maze, the supercell would be the 150x150 maze holding all of those. ↩︎

21. This approach isn’t a bad one; it’s just not one that felt like the right fit for the unfair maze I’m making. Different maze textures will have different feels, and an infinite maze where you can fairly reliably move towards your destination would probably be more enjoyable. ↩︎

22. Look this up for yourself. I’m not going to explain it well. ↩︎

23. This was generated using a little L-systems page I made. It’s a lot to go into here, but it can be fun to mess around with (be sure to look at the examples at the bottom). It’s here. ↩︎

24. Once again, not a mathematician. ↩︎

25. An outcome I want to happen. ↩︎

26. If this has a technical term, I couldn’t find it. ↩︎

27. My cute way of saying that it bridges the divide from a set of finite-dimension cells to an infinite maze. ↩︎

28. There could have been multiple meshes per submaze, allowing more flexibility in generation, but it was a jam and ultimately not a problem I found interesting enough to solve with the time allotted. ↩︎